People think the math for programming a vertical plotter is really hard. Still, I used only second grade high school math to calculate them. I made both Python and EV3-G implementations. Here’s how it works.
Target motor positions

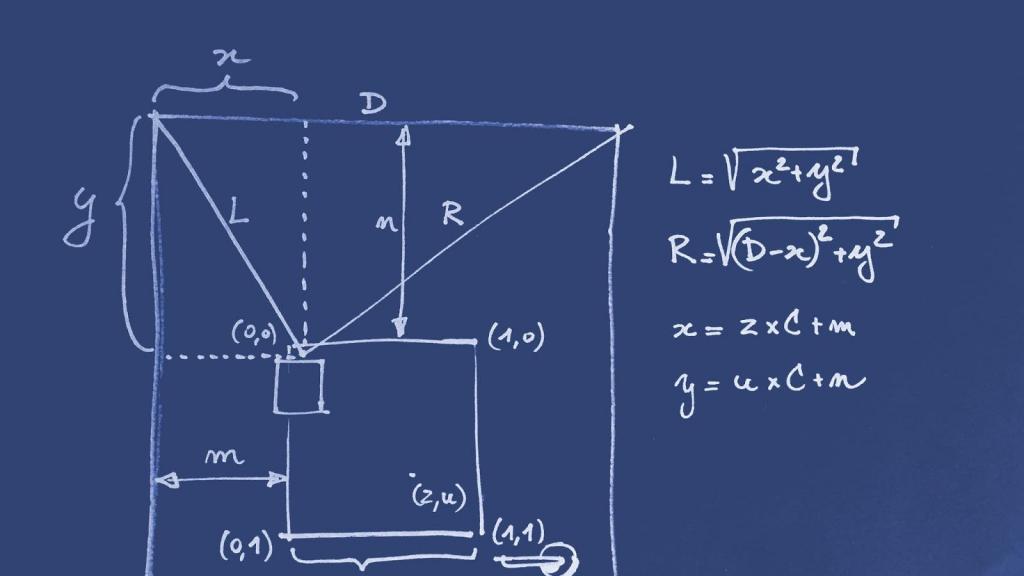
For all calculations I am using a coordinate system with the top left of the door as (0,0) and with cm as units. So the top right of the door is (90,0). The positive y-axis is pointing down so I have only positive numbers.
The first goal is now to calculate the correct lengths of the ropes L and R in terms of the coordinates (x,y) of the target location for the robot. For this you can use Pythagoras. The left rope is the easiest: there is a triangle with sides x,y and L where
[python]L = (x**2 + y**2)**0.5[/python]
(In python the double asterisk means a power). The right rope is also part of a triangle. This triangle has y, 90-x and R as sides. Therefore:
[python]R = ( (90-x)**2 + y**2 )**0.5[/python]
Now that we have the target lengths we have to calculate the degrees the motor has to rotate to reach our desired coordinate. The diameter of the bush is about 0,9 cm. A complete 360 degree rotation results therefore in a 0,6 cm * 3,14 change in length. That is about 170 degrees of rotation to move one centimeter. I mounted the motors so that forward rotation is upwards. Therefore the motor target for the left motor is L * -170, the right target is R * -170.
Navigating the drawing canvas
Now we have a formula to navigate the complete door. But what we really want is to navigate a piece of paper in the middle of the door. I wanted the robot to be usable independently of the space between the attachment points or the size of the paper. Therefore I defined a second coordinate system that has (0,0) in the top left of the paper and is normalised. This means all coordinates are between 0 and 1. This coordinate system is easy to scale on different plotting surfaces and paper sizes. It works like this: let m be the margin left of the paper, n be the margin on top and C the with of the canvas. The coordinates (x,y) in terms of the normalised coordinates (u,v) become simply:
[python]x = C * u + m[/python]
and
[python]y = C * v + n[/python]
At this point it’s simply a matter of reading two files, x.rtf and y.rtf with normalised coordinates and moving the robot towards each of these coordinates.
Ev3 program
You can also download the Lego Mindstorms Ev3 program to see the details. The ev3 main program expects 2 rtf files (robot text files), on named x.rtf and the other y.rtf. Both contain target coordinates. x.rtf has the number of coordinates as it’s first line. Note that you can’t open these files with a Rich Text File editor!
Building instructions
Get the building instructions in the digital download section!






Hallo
de link naar het ev3 programma voor verticale plotter doet het niet, Zou je deze misschien kunnen sturen? Ik wil mn ev3 weer eens oppakken, maar heb me nooit zo in het programmeren ermee verdiept.
groeten
Jeroen
I uploaded the file. Could you let me know if it works? I can’t open it anymore since I on a new MacOS.
The link works fine. Thanks for sharing your work.
Your publication helped me take a giant leap forward in my own development of a (slightly different) vertical plotter implementation.
Can you link to my site or YouTube channel, then?
hallo Anton, is het ook mogelijk om dit te doen met een powered up blok (we hebben de 42410)? ik ben met mijn zoontje aan het bouwen, maar ben niet zo bekend met programmeren. kan dit met het powered up programma of moet dit met pybricks?
Hallo Anton,
Is het ook mogelijk om een vergelijkbaar project te maken met de technic hub (we hebben de 42140)? ik ben met mijn zoontje aan het bouwen maar ben niet heel bekent met programeren. kan dit met de powered up app of moet dit in pybricks?
Dat is zeker mogelijk. Maar niet makkelijk. 😉 probeer eens pybricks.